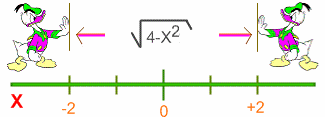
Una función continua es aquella cuya regla
de correspondencia asigna incrementos pequeños en la variable dependiente a
pequeños incrementos de los elementos del dominio de dicha función, es decir, ,
y usando la expresión Δy + y = f(Δx + x), queda donde en este caso, f(x) = y.
Esto quiere decir que , y si este último límite existe significa en consecuencia por
un teorema de límites (un límite existe si y sólo si los dos límites laterales
existen y son iguales) que toda función f(x) que cumpla con
es continua en el punto a.
Para que una función sea continua debe serla
en todos los puntos de su dominio (donde esta definida).
Para ser continua en
un punto, el valor de la funcion en dicho punto debe ser igual al límite de la
función en el mismo.
f(a) = lim f(x) = lim f(x)
Continuidad en un punto: Una funcion´ f es continua en a si se verifican las siguientes condiciones:
1. f(a) esta definida. 2. ´ limx→a
f(x) existe. 3. limx→a
f(x) = f(a).
Continuidad en un intervalo abierto: Una funcion´ f se dice continua en un intervalo abierto (b, c) si lo es en
todos los puntos de ese intervalo.
Si f es continua en toda la recta real (−∞, ∞) diremos simplemente que f es una funcion continua ´ . Se dice que
f es discontinua en a si no es continua en dicho punto.
Continuidad por la derecha: Una funcion´ f es continua por la derecha en a si se verifican las siguientes condiciones:
1. f(a) esta definida.
2. ´ lim x→a+ f(x) existe.
3. lim x→a+ f(x) = f(a).
Continuidad por la izquierda: Una funcion´ f es continua por la izquierda en a si se verifican las siguientes
condiciones:
1. f(a) esta definida.
2. ´ lim x→a− f(x) existe.
3. lim x→a− f(x) = f(a).
Continuidad en un intervalo cerrado: Una funcion´ f se dice continua en un intervalo cerrado [b, c] si es continua
en (b, c) y tambien es continua por la derecha en ´ b y por la izquierda en c



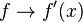

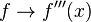
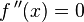
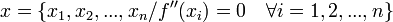
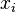 sustituyendo la variable dependiente en la función.
sustituyendo la variable dependiente en la función.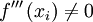 , se tiene un punto de inflexión en
, se tiene un punto de inflexión en 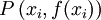 .
.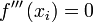 , debemos sustituir
, debemos sustituir